Python机器学习三大件之一numpy

2021-08-20 14:55:20 浏览数 (4)

在机器学习中，numpy被称为python机器学习的三大件之一，原因很简单，机器学习的很多内容都建立在矩阵运算上，而numpy是python中矩阵运算做得比较好的一个科学计算库，所以机器学习离开不了numpy，今天我们就来介绍一下numpy这个机器学习的大件吧。

一、前言

机器学习三大件：numpy， pandas， matplotlib

Numpy（Numerical Python）是一个开源的Python科学计算库，用于快速处理任意维度的数组。

Numpy支持常见的数组和矩阵操作。对于同样的数值计算任务，使用Numpy比直接使用Python要简洁的多。

Numpy使用ndarray对象来处理多维数组，该对象是一个快速而灵活的大数据容器。

NumPy提供了一个N维数组类型ndarray

import numpy as np
score = np.array(
[[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]])

score

array([[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]])

Numpy专门针对ndarray的操作和运算进行了设计，所以数组的存储效率和输入输出性能远优于Python中的嵌套列表，数组越大，Numpy的优势就越明显。

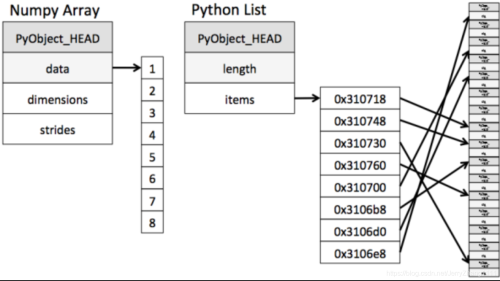
在这里插入图片描述

从图中我们可以看出ndarray在存储数据的时候，数据与数据的地址都是连续的，这样就给使得批量操作数组元素时速度更快。
list – 分离式存储,存储内容多样化
ndarray – 一体式存储,存储类型必须一样
ndarray支持并行化运算（向量化运算）
ndarray底层是用C语言写的,效率更高,释放了GIL

二、基本操作

# 生成0和1的数组
ones = np.ones([4,8])
ones

array([[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.]])

# 生成等间隔的数组
np.linspace(0, 100, 11)

array([ 0., 10., 20., 30., 40., 50., 60., 70., 80., 90.,
100.])

#创建等差数组 — 指定步长
np.arange(10, 50, 2)

array([10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48])

三、正太分布

  • rand函数根据给定维度生成[0,1)之间的数据，包含0，不包含1
np.random.rand(4,2)

array([[ 0.02173903, 0.44376568],
[ 0.25309942, 0.85259262],
[ 0.56465709, 0.95135013],
[ 0.14145746, 0.55389458]])

  • randn函数返回一个或一组样本，具有标准正态分布
np.random.randn(2,4)

array([[ 0.27795239, -2.57882503, 0.3817649 , 1.42367345],
[-1.16724625, -0.22408299, 0.63006614, -0.41714538]])

  • randint返回随机整数，范围区间为[low,high），包含low，不包含high
np.random.randint(1,5) # 返回1个[1,5)时间的随机整数

4

  • 生成均匀分布的随机数，举例1：生成均值为1.75，标准差为1的正态分布数据，100000000个
x1 = np.random.normal(1.75, 1, 100000000)

array([2.90646763, 1.46737886, 2.21799024, …, 1.56047411, 1.87969135, 0.9028096 ])

  • 均匀分布
# 生成均匀分布的随机数
x2 = np.random.uniform(-1, 1, 100000000)

array([ 0.22411206, 0.31414671, 0.85655613, …, -0.92972446, 0.95985223, 0.23197723])

四、数组的索引、切片

# 三维
a1 = np.array([ [[1,2,3],[4,5,6]], [[12,3,34],[5,6,7]]])
# 返回结果
array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[12,  3, 34],
        [ 5,  6,  7]]])
# 索引、切片
a1[0, 0, 1]   # 输出: 2

五、形状修改

stock_change.reshape([5, 4])  #5*4
stock_change.reshape([-1,10])  #2*10，-1: 表示通过待计算

六、转置

stock_change.T.shape

七、类型转换

arr = np.array([[[1, 2, 3], [4, 5, 6]], [[12, 3, 34], [5, 6, 7]]])
arr.tostring()

八、数组的去重

temp = np.array([[1, 2, 3, 4],[3, 4, 5, 6]])

>>> np.unique(temp)
array([1, 2, 3, 4, 5, 6])

逻辑运算
直接进行大于,小于的判断：test_score > 60
合适之后,可以直接进行赋值：test_score[test_score > 60] = 1
通用判断函数
np.all() np.all(score[0:2, :] > 60)
np.any() np.any(score[0:2, :] > 80)
统计运算
np.max()
np.min()
np.median()
np.mean()
np.std()
np.var()
np.argmax(axis=) — 最大元素对应的下标
np.argmin(axis=) — 最小元素对应的下标

九、广播机制

  • 数组运算,满足广播机制,就OK

1.维度相等

2.shape(其中对应的地方为1,也是可以的)

arr1 = np.array([[0],[1],[2],[3]])
arr1.shape
# (4, 1)

arr2 = np.array([1,2,3])
arr2.shape
# (3,)

arr1+arr2
# 结果是：
array([[1, 2, 3],
       [2, 3, 4],
       [3, 4, 5],
       [4, 5, 6]])

到此这篇Python机器学习三大件之一——numpy的使用介绍就介绍到这了,更多python学习内容请搜索W3Cschool以前的文章或继续浏览下面的相关文章。

Python

0 人点赞